Prime Number ตัวเลขแปลก ๆ กับการเข้ารหัส

Prime Number หรือ จำนวนเฉพาะ เป็นจำนวนที่มีความพิเศษมาก ๆ เราอาจจะเริ่มได้ยินตอนเราอยู่ประถมแล้วละ ตอนนั้น เราก็ยังสงสัยนะว่า กูเรียนไปทำไมวะ เรียนไปแล้วมันได้บ้าอะไร เพราะตอนนั้นไม่มีใครบอกนะว่า มันเอามาทำอะไรได้ แต่บอกว่า มันคืออะไร แต่พอมาเรียนพวก Cyptographic ทำให้รู้ว่า เชี้ย !! แมร่งเป็น Core เลยนิหว่า วันนี้เรามาเล่ากันแบบสนุก ๆ ละกัน

Prime Number คืออะไร ?

เอาหล่ะ เรามาทบทวน เกี่ยวกับ Prime Number หรือจำนวนเฉพาะกันก่อนดีกว่า ถ้าเราจำได้ คร่าว ๆ จำนวนเฉพาะ ก็คือ จำนวน ที่ ตัวมันเอง และ 1 หารลงตัว หรือพูดอีกนัยคือ ไม่ว่า เราจะเอาจำนวนอะไรไปหาร จะต้องมีเศษ ยกเว้น ตัวมันเอง และ 1 นั่นเอง

ถามแบบ ขำ ๆ เลย คิดว่า 1 เป็น Prime Number มั้ย เพราะ 1 หาร 1 ลงตัว และ 1 ก็หาร 1 ลงตัว ?

เฉลยเลยละกัน 1 ไม่ได้เป็น จำนวนเฉพาะ เพราะ ถ้าเราพูดถึงนิยามของ จำนวนเฉพาะ เราบอกว่า เป็นตัวจำนวนเต็มอะไรสักอย่างที่ เอามาหารตัวมันเอง และ 1 ลงตัว จะเห็นว่า มันเป็นตัวเลขที่สามารถหารลงตัวได้ 2 ตัวเลขด้วยกัน แต่ 1 มันหาร 1 ลงตัว แต่อ้าว อีกตัวก็เป็น 1 เหมือนกัน มันเลยไม่ได้เป็นจำนวนเฉพาะ งง มะ ถถถถถ

ดังนั้นจำนวนที่เล็กที่สุดที่เป็น จำนวนเฉพาะ ก็น่าจะเป็น 2 ใช่มั้ยฮะ นั่นง่าย ๆ เลย แต่ถ้าเราถามว่า แล้วจำนวนที่มากที่สุดที่เป็นจำนวนเฉพาะละ อื้มมม น่าสนใจกว่าใช่มะ จริง ๆ แล้ว Euclid เคยพิสูจน์แล้วนะว่า มันไม่มีจำนวนเฉพาะที่มากที่สุด เพราะเรากำลังพูดถึงจำนวนเต็ม ซึ่งมันไปได้เรื่อย ๆ แบบไม่มีที่สิ้นสุด เลยทำให้มันไม่มีจำนวนเฉพาะที่มากที่สุด เพราะเราไม่รู้ว่ามันไปสิ้นสุดที่ไหน

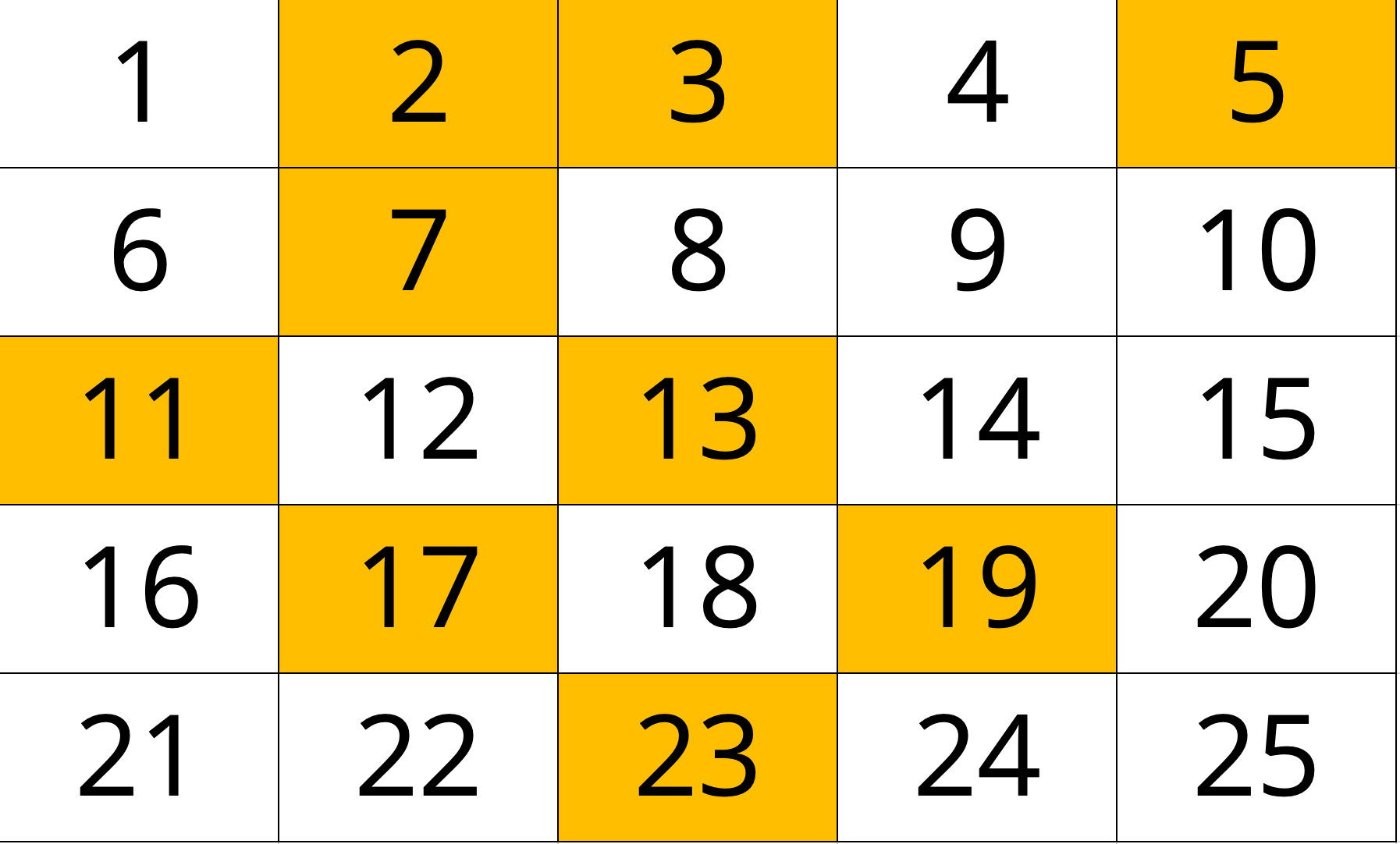
แต่ ๆ ถ้าเราลองไล่จำนวนเฉพาะออกมา แล้วเราลองสังเกตกันดูนะ ตัวแรก ๆ คือ 2 และ 3 แล้วตัวต่อไป 5 ซึ่งความห่างมันไม่เท่าละ หรือ ถ้าเราไปไกล ๆ หน่อย เอาสัก 13 แล้วตัวต่อไปเป็น 17 เราสังเกตอะไรมั้ย เราจะเห็นได้ว่า เมื่อเราหาจำนวนเฉพาะไปไกลมากขึ้นเรื่อย ๆ จำนวนเฉพาะมันจะมีน้อยลงเรื่อย ๆ และ หายากขึ้นเรื่อย ๆ ทำให้การหาจำนวนเฉพาะเป็นอะไรที่ท้าทายมาก ๆ โดยเฉพาะถ้าเราอยากจะหาในจำนวนขนาดใหญ่

Finding Prime Number

อย่างที่เราบอกว่า การหา จำนวนเฉพาะ เป็นเรื่องที่ท้าทายมาก ๆ เราลองมาหามันกันเองดีกว่า

def find_prime_brute_force (max_num : int) -> list[int] :
    prime_numbers = []

    for i in range(2,max_num+1) :
        is_prime = True

    	# Determine whether this number is prime or not
        for j in range(2,i) :
            if i % j == 0 :
                is_prime = False
                break

        if is_prime :
            prime_numbers.append(i)

    return prime_numbers

ถ้าเราคิดตรง ๆ เล่น Brute force ไปเลย เราลองเขียนออกมาเป็น Function สักตัวละกัน เราเริ่มจากการสร้าง List เพื่อเก็บคำตอบชื่อ prime_numbers จากนั้น เรามาที่ส่วนของการคิดของเราง่าย ๆ เลยคือ เรา Loop ตั้งแต่ 2 จนไปถึงจำนวนที่เราตั้งไว้เพื่อหาแล้วบวก 1 เพราะใน Loop มันจะเอาตั้งแต่ 0 ถึงจำนวนที่เราใส่ลบ 1

อะไรไม่รู้ เราก็บอกไว้ก่อนเลยว่า จำนวนนี้เป็น จำนวนเฉพาะนะ ผ่าน Flag ตอนนี้เราต้องย้อนกลับไปที่นิยามของจำนวนเฉพาะแล้วคือ เป็นจำนวนที่ 1 และ ตัวของมันเอง หารลงตัวเท่านั้น ดังนั้น เราจะต้องพิสูจน์ให้ได้ว่า ไม่มีจำนวนไหนเลย นอกจาก 1 และตัวมันเองหารลงตัว ทำให้เราจะต้อง Loop ในนั้นอีก แล้วก็เอามา Modulo หรือหารเอาเศษกัน ถ้ามันหารลงตัว คือการหารแล้วไม่มีเศษ ถ้าเกิดแบบนั้นจริง เราก็จะตั้ง Flag เป็น False ไป กับ เรา Break ออกจากการหาได้เลย เพราะ เพียงแค่จำนวนใดจำนวนหนึ่ง นอกจาก 1 และตัวมันเองหารลงตัว ก็คือจบเลย สุดท้าย ถ้ามัน Loop ผ่านมาได้หมด Flag จะยังไม่เปลี่ยน เราก็ดัก Guard ไว้ เพื่อเพิ่มจำนวนนั้น ลงไปใน List คำตอบของเรา แล้วเมื่อ Loop เสร็จ เราก็ Return มันกลับไป

เรามาลองวิเคราะห์ Algorithm นี้กันหน่อย ถ้าเราดูคร่าว ๆ เลย เราจะเห็นว่า มันมี O(n^2) เลยทีเดียว จาก Loop ทั้งหมด 2 ชั้น ชั้นแรกคือ เรา Loop เพื่อวนจำนวนที่เราต้องการหา และอีกชั้นที่ลึกลงไปคือส่วนที่เราเอามาลองหารไปเรื่อย ๆ ถ้าเราเอามาหาจำนวนไม่กี่ตัว มันก็ไม่น่ามีปัญหา แต่ถ้าเราเอามาหาจำนวนขนาดใหญ่ ๆ แบบนี้เริ่มไม่น่ารักแล้วใช่มั้ย งั้นเรามีวิธีที่ดีกว่านี้มั้ย

def find_prime_a_bit_better (max_num : int) -> list[int] :
    prime_numbers = []
    
    for i in range(2, max_num+1) :
        is_prime = True

        for j in prime_numbers :
            if i % j == 0 :
                is_prime = False
                break

        if is_prime :
            prime_numbers.append(i) 
               
    return prime_numbers

เราลองปรับปรุงอีกหน่อย ถ้าเราลองสังเกตจำนวนที่ไม่ได้เป็นจำนวนเฉพาะสักหน่อย เช่น 4 ไม่ได้เป็นจำนวนเฉพาะ เพราะว่า มันเกิดจาก 2 x 2 หรือ ถ้าเราเอา 6 บ้าง มันก็เกิดจาก 3 x 2 เราจะสังเกตว่า จำนวนอะไรสักอย่างที่ไม่ได้เป็นจำนวนเฉพาะ ถ้าเราเอามา Decompose เราจะเห็นว่า ไม่ว่ายังไง มันก็จะเกิดจากผลคูณของจำนวนเฉพาะอย่างน้อย 2 ตัวเข้าด้วยกัน

ถ้าเป็นแบบนั้น ตอนที่เราไล่หารเช็คทุกตัว เราไม่น่าจะจำเป็นต้องทำแบบนั้นซะทีเดียวใช่มะ เราก็เอาจำนวนเฉพาะที่เราเคยหาเจอมาหารเข้าไปเช็ค ก็จบแล้ว นั่นแปลว่า เราลดจำนวนตัวเลขที่เราต้องหารเช็คไปเยอะเลย

Algorithm ดูดีนะ เราลงรันออกมา เอาจำนวนที่มันน่าจะพอเห็นชัด ๆ หน่อย ที่สัก 10,000 ตัวไปเลย วิธีแรกที่เรา Brute Force ออกมา เราใช้ 0.1833 วินาที และ วิธีที่เราปรับ เราใช้ 0.0198 วินาที ตีขำ ๆ ก็ 9 เท่ากว่า ๆ ได้ แค่เราพยายาม Scope จำนวนที่หา ก็ทำให้ความเร็วมันได้มากขึ้น จริง ๆ วิธีนี้ เราก็เอามาใช้กับพวกงาน AI เหมือนกันไว้มาเล่าวันหลัง

เราลองมาดู Big-O กันหน่อยดีกว่า เราลอง Plot เทียบขำ ๆ มาดูกัน เพื่อให้เทียบแล้วเข้าใจได้ง่ายขึ้น เราเอา O(n), O(nlogn) และ O(n^2) ใส่เข้ามาด้วย เราจะเห็นว่า ไม่ว่าจะวิธีไหนก็ตาม มันก็จะยังน้อยกว่า n^2 แหละ แต่ ๆๆๆ ถ้าเราเอาทั้ง 2 วิธีนี้มาเทียบจริง ๆ เห็นได้เลยว่า วิธีการที่เราจำกัดตัวเลข มันช่วยได้เยอะมาก ๆ มันเกือบจะลงไปเท่ากับ O(nlogn) อยู่แล้ว มันก็จะไปตรงกับเวลาที่เราได้มานั่นเอง

ถ้าใครที่เรียนมา อ่านวิธีที่ 2 ของเรา อาจจะเอ๊ะ ๆ ว่า เห้ย มันคล้าย ๆ กับ Sieve of Eratosthenes เลย มันเป็น Algorithm ที่โคตรเก่าแก่มาก ๆ วิธีนั้นมีแนวคิดคล้าย ๆ กันคือ เรารู้ว่า อะไรที่คูณด้วยจำนวนเฉพาะลงตัว จะไม่ได้เป็นจำนวนเฉพาะ เราก็แค่ค่อย ๆ ขีดฆ่าออกไปเรื่อย ๆ เมื่อเราทำแบบนี้ไปเรื่อย ๆ จำนวนที่ไม่ได้โดนขีดฆ่า นั่นแหละคือจำนวนเฉพาะ ถ้าเราหา จำนวนเฉพาะในจำนวนที่ไม่ใหญ่มาก วิธีนี้ก็เป็นวิธีที่ดีเลยละ

แต่วิธีที่ใหม่ ๆ หน่อยพวก Sieve of Atkin พวกนี้ก็จะเร็วขึ้นอีก ลองไปหาอ่านดูได้ วิธีมันคือแบบ ซับซ้อน และ พีค ๆ เข้าใจยากกว่าเดิมหน่อย แต่ก็เร็วกว่าเดิมมาก ๆ ลองไปหาอ่านดูได้ เราไม่ขอเล่าละกัน รู้สึกว่าเริ่มจะยาวขึ้นเรื่อย ๆ แล้ว

The Largest Prime Number So Far.....

เราบอกไปว่า การหาจำนวนเฉพาะยิ่งจำนวนเยอะ ยิ่งหายากขึ้นเรื่อย ๆ ถามว่า แล้วตอนนี้ โลกของเรา เรารู้จำนวนเฉพาะที่ใหญ่ที่สุดอยู่ที่เท่าไหร่ ใช่ฮะ มันมีคนมานั่งหา และเก็บพวกสถิติของการหาจำนวนเฉพาะด้วยนะ คือ Great Internet Mersenne Prime Search (GIMPS) เราชอบเรียกขำ ๆ ว่า กิ๊มส์

ถ้าเราเคยดูพวกการ Benchmark พวก CPU ต่าง ๆ หนึ่งในเครื่องมือในการ Benchmark ก็น่าจะเคยได้ยินโปรแกรมที่ชื่อว่า Prime95 โปรแกรมนี้แหละ เขาใช้ในการเอามาหาค่าจำนวนเฉพาะกันจริง ๆ ในคอมพิวเตอร์นะ ไม่ได้เป็นแค่โปรแกรมในการ Benchmark เท่านั้น พวกจำนวนเฉพาะที่หาได้ใหม่ ๆ ที่ GIMPS เก็บไว้ หลัง ๆ ก็มาจากโปรแกรม Prime95 ทั้งนั้น

ณ วันที่เขียนตอนนี้ จำนวนเฉพาะที่เราหาได้ล่าสุด เจอในวันที่ 7 Dec 2018 นี่แหละ ห่างจากตอนนี้ 4 ปีแล้ว จำนวนของมันอยู่ที่ 2 ยกกำลัง 82,589,933 ลบอีก 1 พวกนี้เราเรียกว่า Mersenne Primes ลองไปหาอ่านเพิ่มดูได้ ๆ

สรุปแล้ว Prime Number เกี่ยวอะไรกับ Encryption

Encryption หรือการเข้ารหัส เป็นกระบวนการหนึ่งที่เปลี่ยนแปลงข้อมูลของเราให้อยู่ในรูปที่คนทั่ว ๆ ไปอ่านไม่ได้ และ สามารถแปลงกลับได้โดยคนที่รู้เท่านั้น เป็นกระบวนการที่มีความสำคัญมาก ๆ ในโลก โดยเฉพาะอินเตอร์เน็ตที่เราอาจจะโดนใครไม่รู้ล้วงข้อมูลไปเมื่อไหร่ก็ได้

การเข้ารหัส โดยทั่ว ๆ ไป เราจะทำกันอยู่ 2 การกระทำหลัก ๆ คือ การเข้ารหัส และ การถอดรหัส โดยที่เรามีข้อมูลที่เราต้องการจะส่งให้ปลายทาง เราก็จะทำการเข้ารหัสข้อมูลนั้น แล้วส่งไปที่ปลายทาง เมื่อปลายทางได้รับ ถ้าอ่านตรง ๆ เลย ก็อาจจะ งง ว่า มันส่งอะไรมาวะ แต่ถ้าเราทำการถอดรหัสออกมา เราก็จะได้ข้อมูลเดียวกับที่ต้นทางส่งมานั่นเอง

ความท้าทายมันอยู่ที่ ในการเข้ารหัส วิธีการเป็นอะไรที่ไม่ได้เป็นความลับอะไร แต่สิ่งที่เป็นความลับคือ Key หรือกุญแจในการเข้าและถอดรหัส เหมือนกับ ทุก ๆ วันที่เราใช้กุญแจ ทุกคนรู้นะว่า กุญแจทำงานยังไง มันไขแล้วปลดล๊อคได้ยังไง แต่ความยากอยู่ที่ เขี้ยวมันดอกกุญแจ

ในแง่ของการเข้ารหัสในคอมพิวเตอร์ มันเป็นเรื่องของคณิตศาสตร์เลย ถ้าใครที่มาเรียนจะเห็นเลยว่า คณิตศาสตร์เป็นอะไรที่โคตรเจ๋ง มันสวย มัน Sexy มาก ๆ โอเคนอกเรื่องไปไกลละ กลับมา ถามว่า จำนวนเฉพาะเกี่ยวอะไร

เราใช้จำนวนเฉพาะในการเอามาสร้างดอกกุญแจในการเข้าและถอดรหัสนี่แหละ ถามว่าทำไม?? เราก็ต้องย้อนกลับไปในประโยคที่เราบอกว่า การหาจำนวนเฉพาะมันเป็นเรื่องที่ใช้พลังในการประมวลผลสูงมาก ๆ แต่ การเอาจำนวณเฉพาะคูณกัน เป็นเรื่องง่ายมาก ๆ มองกลับกันถ้าเราบอกว่า เรามี 2 ฝั่ง ต่างสุ่มจำนวนเฉพาะ เช่น 23 และ 29 โดยสมมุติว่า กุญแจเกิดจากผลคูณ กลายเป็น 667

ถ้าเราพยายาม Decompose ออกมาให้ได้ เราก็จะทำได้แค่ 23 x 29 เท่านั้นแหละ ไม่สามารถเป็นตัวเลขอื่นได้แล้ว แต่ปัญหาคือ ถ้าเกิดเป็นใครไม่รู้เลย ไม่รู้ตัวเลข แต่พยายามที่จะหากุญแจนี้ให้ได้ เขาก็ต้องนั่งพยายามหา จำนวนเฉพาะอะไรไม่รู้มาคูณกันแล้วให้ได้เป็นกุญแจสักดอกที่ถอดรหัสได้ ในความเป็นจริง เราไม่ได้ใช้ตัวเลขน้อยขนาดนี้ เราใช้ตัวเลขขนาดใหญ่มาก ๆ

ทำให้การหา มันเป็นเรื่องยาก เลยทำให้การใช้จำนวนเฉพาะ ทำให้การเข้ารหัส และ ถอดรหัสมันง่าย แต่การสุ่มกุญแจ มันยากนั่นเองลองไปหาอ่านเพิ่มได้ พวก RSA และ Diffie-Hellman Key Exchange