ทำไม 0.3 + 0.6 ถึงได้ 0.8999999 กับปัญหา Floating Point Approximation

อ่านชื่อหัวเรื่องมา เราว่านักคณิตศาสตร์กำหมัดแล้วนะ แต่ลองดูกันได้ เอา 0.3 + 0.6 ด้วยเครื่องคอมพิวเตอร์ ลองทำผ่าน Python ขำ ๆ ดูก็ได้ เราจะเห็นว่า มันจะได้ออกมาเป็น 0.89999 ไปเรื่อย ๆ เลย ทั้ง ๆ ที่จริง ๆ แล้ว เราบวกเอง มันก็ควรจะได้ 0.9 เป๊ะ ๆ ซึ่งเรื่องนี้ มันเกิดจากสิ่งที่เรียกว่า Floating Point Approximantion บนเครื่องคอมพิวเตอร์นั่นเอง

Floating Point Representation in Computer

เนื่องจากเครื่องคอมพิวเตอร์ มันเป็นเครื่องที่ทำงานบนระบบเลขฐานสอง ไม่ได้ใช้เลขฐานสิบเหมือนที่เราใช้งานกัน ฟิล ๆ เหมือนกับ เราคุยคนละภาษากัน ดังนั้น เลขที่เราเห็นเป็นฐานสิบ จริง ๆ แล้ว เวลาเครื่องคอมพิวเตอร์มันเก็บ มันก็จะเก็บเป็นฐานสองอยู่ดี

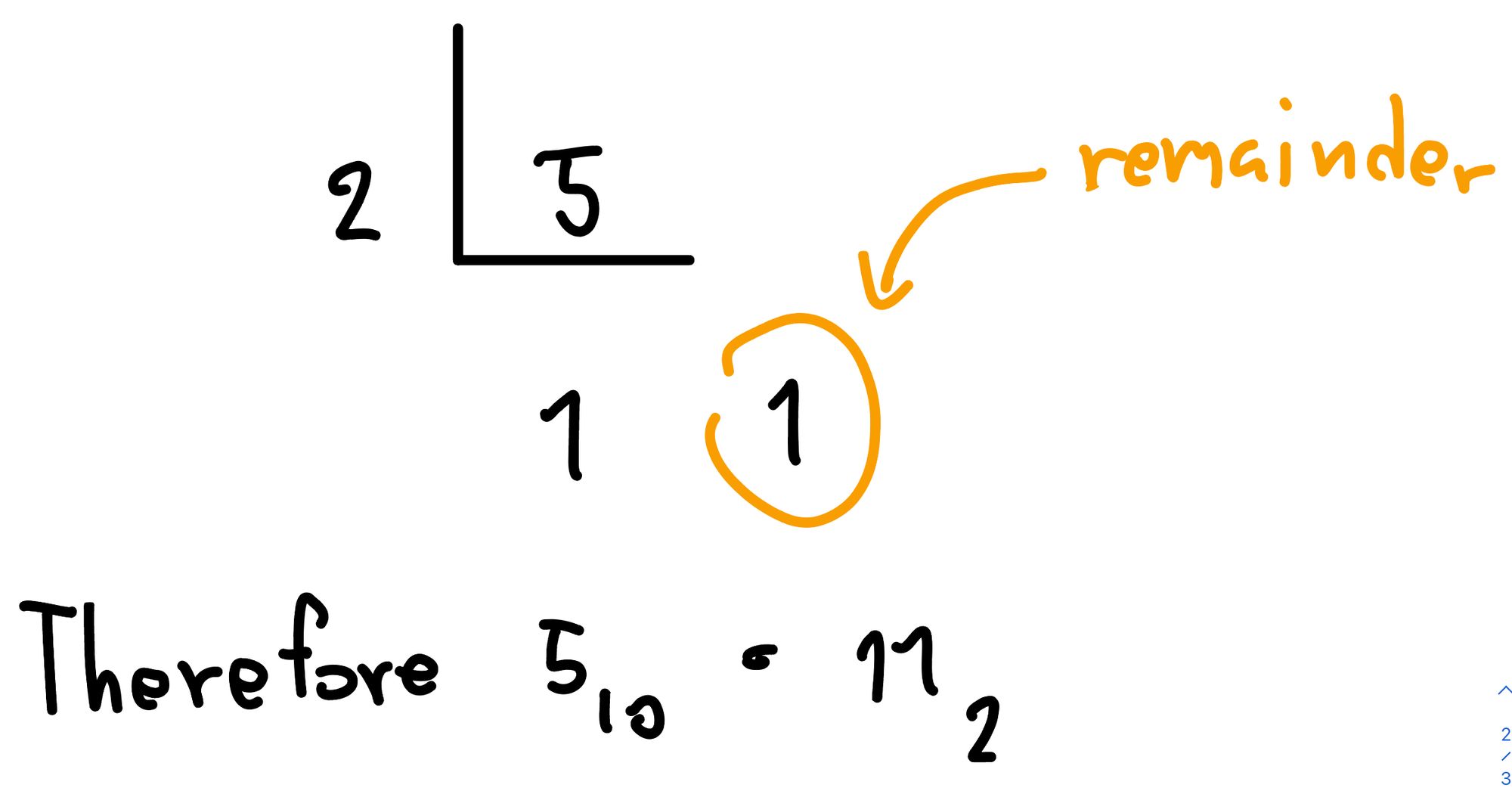
ซึ่งการแปลงเลขฐานเป็นเรื่องไม่ยากเท่าไหร่เนอะ เรียนกันตั้งแต่ประถมแล้ว เช่นเราบอกว่า เราจะแปลง 5 ฐาน 10 ให้กลายเป็นฐาน 2 ก็จะเป็น 11 ใช่มะ เพราะเรา เอา 5 หาร 2 ได้ 1 แล้วเหลือเศษ 1 ก็เลยกลายเป็น 11

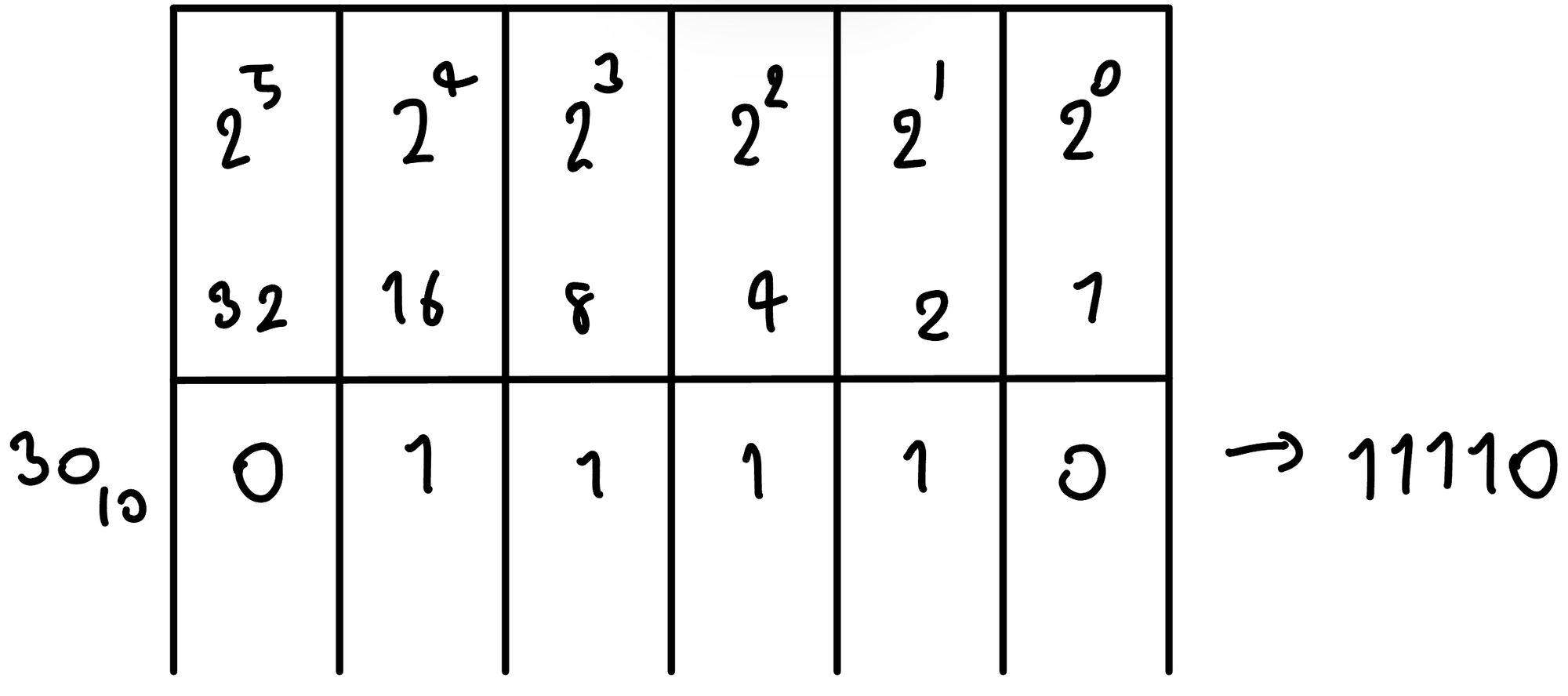
หรืออีกวิธีที่เราใช้เยอะมาก ๆ เวลาเรานับเร็ว ๆ คือ เราจำสองกำลังได้ คือ 1,2,4,8,16,32 ไปเรื่อย ๆ ถ้าเราบอกว่า จะเอา 30 มันมากกว่า 16 แต่น้อยกว่า 32 ทำให้ 16 ต้องเป็น 1 จากนั้นเอา 16 ไปลบ มันจะเหลือ 14 ก็มากกว่า 8 ทำให้ตำแหน่งของ 8 ต้องเป็น 1 จากนั้นจะเหลือ 6 ก็ไปลง 2 กับ 4 ได้เลย เท่านี้เองก็จะได้เลขออกมาแล้ว จะเป็น 11110

ถามว่า แล้วถ้าเป็นจุดทศนิยมละ เราจะทำยังไง ก็หลักการเดียวกัน เราก็คือ ยกกำลังติดลบ มันก็คือ 1 ส่วน 2 กำลัง อะไรก็ว่าไป มันก็ไล่ลงไปตั้งแต่ 0.5, 0.25, 0.125, 0.0625 ไปเรื่อย ๆ เลย เช่น 0.4 ก็จะแทนได้ด้วย 0.0110 0110 0110 0110 0110 0110 0 ฐานสอง ก็เรียบร้อย

ทีนี้ เวลาเราเก็บจริง ๆ เราจะต้องเก็บทั้งจำนวนเต็มด้านหน้า และจุดทศนิยมด้วย พร้อมกับเครื่องหมาย บวก หรือ ลบอีก ซึ่งมันเก็บได้หลายวิธีมาก ๆ เป็นเรื่องที่ไม่ดี เพราะไม่งั้น แต่ละคนเก็บกันคนละแบบ เวลาอ่านก็แย่เลย ต้องมานั่ง Convert อะไรอีกเสียเวลา

ในการเก็บข้อมูล ที่เราเคยได้ยินเครื่องคอมพิวเตอร์แบบ 32 หรือ 64-Bits ก็คือตรงนี้แหละ ถ้าไปหาอ่านเพิ่มลองหา IEEE-754 มันเป็นมาตรฐานสำหรับการ Represent พวกตัวเลขบนเครื่องคอมพิวเตอร์ พูดง่าย ๆ มันจะใช้ Scientific Notation เช่น 134.21 มันจะแปลงเป็น 1.3421 x 10^ 2

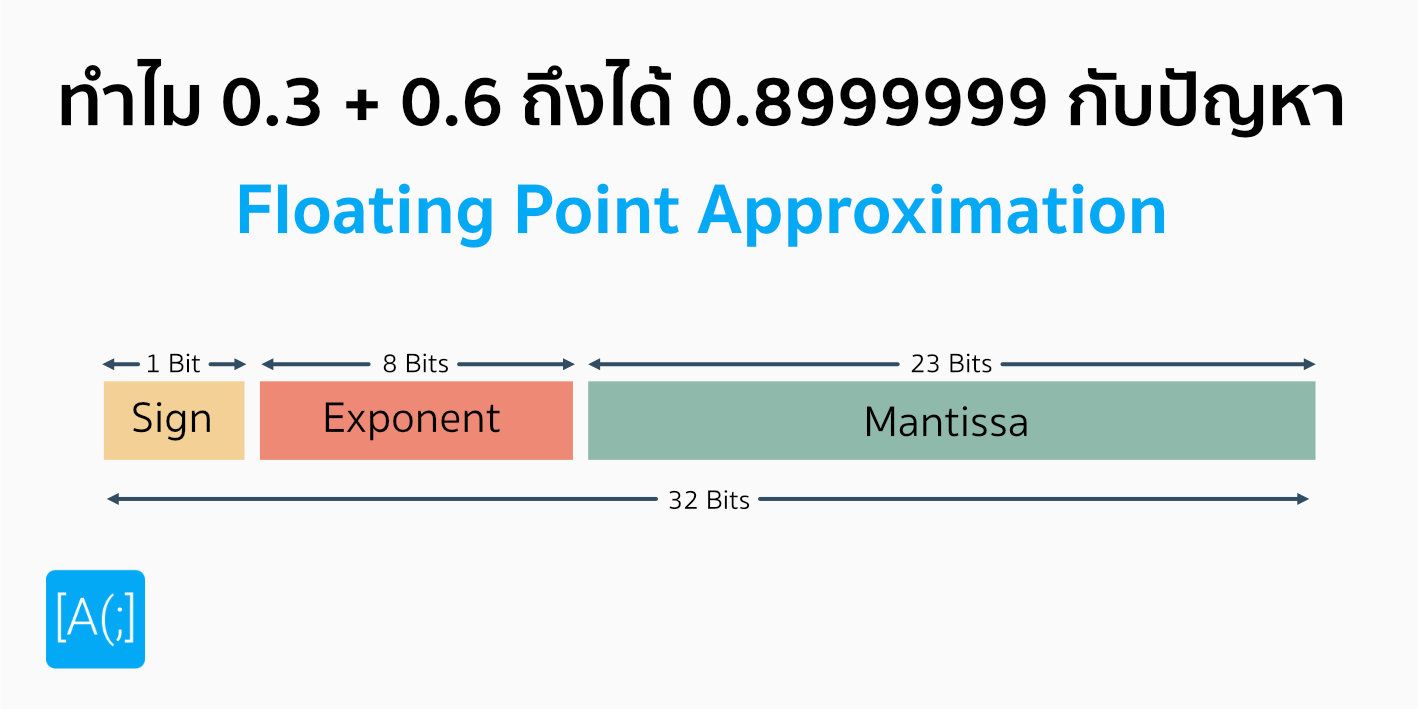
จากนั้น ดูจากภาพด้านบนนี้ เราจะเห็นว่า วิธีการเก็บมันจะแบ่งส่วนการจัดเก็บออกเป็น 3 ส่วนด้วยกัน คือ Sign Bit, Exponents และ Mantissa โดยจะแบ่งเป็น 1,8 และ 23 ตามลำดับ วิธีการทำก็คือ เมื่อเราแปลงตัวเลขของเราให้อยู่ในรูปแบบของ Scientific Notation เริ่มจากเครื่องหมาย หรือ Sign Bit ถ้าเป็นลบก็แทน 1 แต่กรณีนี้ เป็นบวก เราก็แทน 0 เข้าไป

จากนั้นฝั่งของ Exponent เราได้เป็นกำลัง 2 มา แต่เราจะใส่ 2 ตรง ๆ ไม่ได้ เพราะเราต้องการที่จะทำให้มันสามารถเก็บค่าได้แค่กำลังที่เป็นบวกเท่านั้น ถ้าเราใช้ 8 Bits เราก็เอากึ่งกลาง 127 ไปบวกนั่นเอง ก็จะเป็น 129 ก็จะแทนด้วย 10000001

และท้ายสุดแปลงด้านหลังทศนิยมให้เป็นฐาน 2 อย่างที่เราเล่าไป มันก็จะได้ 0011 0101 1100 0010 1000 1111 นี่แหละคือการที่เครื่องมันเก็บทศนิยม แต่ถ้าเราเก็บแบบ Double Precison มันก็จะใช้ขนาด 64-Bits แบ่งเป็น 1,11 และ 52 สำหรับ Sign Bit, Exponent และ Mantissa ตามลำดับ

ทำไม 0.3 + 0.6 ถึงเป็นปัญหา

ทีนี้ ถามว่า แล้วทำไมเลข 0.3 + 0.6 มันเป็นปัญหา ถ้าเราลองเอาไปบวกกันจริง ๆ อาจจะผ่าน Python Shell ก็ได้ เราจะได้ 0.8999999999999999 แล้วไปเรื่อย ๆ เลย กลายเป็นว่า ชิบหาย แล้วค่ามันก็ไม่ตรงน่ะสิ ยิ่งถ้าเราเอาไปใช้ในการคำนวณต่อด้วย

value = 0.9
digit_count = 17
base_2 = ""

for i in range(digit_count) :
    num = 1 / (2 ** (i+1))
    
    if value > num :
        base_2 += '1'
        value -= num
    else :
        base_2 += '0'

print(base_2)

ถ้าเราลอง Represent 0.9 ในฐาน 2 กัน แต่ขี้เกียจทำมือแล้ว เราเขียน Python Script ขึ้นมาง่าย ๆ กัน คุณภาพไว้ก่อนนะ เอาให้ง่าย ๆ ก่อน เราจะกำหนดค่า value คือค่าที่เราอยากจะ Represent ในที่นี้คือ 0.9 แล้วกำหนด digit_count คือจำนวนตำแหน่งของผลลัพธ์บนเลขฐาน 2 เป็น 17 ทำไมเดี๋ยวเรามาเล่าอีกที และสุดท้าย ทำการ Initiate base_2 ซึ่งเป็นผลลัพธ์ของเรากัน

ใน Loop เราก็จะทำการคำนวณ 2 กำลังลบเท่าไหร่ก็ว่ากันไป แล้วเทียบเลย ถ้ามากกว่า Bit นั้นก็จะ On แล้วเราก็เอามาลบกับค่าจริงของเรา หรือถ้าไม่ ก็จะ Off ไปแล้วใส่ 0 ก็คือ การหารเลขฐานปกตินั่นแหละ แล้วสุดท้ายจบ Loop เราก็ Print ออกมา อีซี่..........

11100110011001100

เราได้ผลลัพธ์มาแล้ว เราอยากให้ลองสังเกตดี ๆ มันจะเริ่มจาก 11100 ก่อน อันนี้ไม่มีอะไร แล้วเราลองดูอีก 4 ตำแหน่งต่อไป มันจะเป็น 1100 แล้วอีก 4 ตำแหน่งต่อไปคือ 1100 เห้ย มันเหมือนกันเลยนี่หว่า มันก็จะวนซ้ำแบบนี้ไปเรื่อย ๆ

แต่ปัญหาคือ จำที่เราคุยกันเรื่องวิธีการ Represent Floating Point บนคอมพิวเตอร์ได้ใช่มะ เรามี Bit ที่เก็บ Mantissa ได้จำกัด เราไม่สามารถเก็บเลขซ้ำแบบนี้ไปเรื่อย ๆ ไม่มีที่สิ้นสุดได้ ดังนั้น ตอนขาที่เราแปลงกลับมา มันก็จะไม่ได้เลขเป๊ะ ๆ ใช่ม้าา

base_2 = '11100110011001100'
base_10 = 0

for position, digit in enumerate(base_2) :
    num = 1 / (2 ** (position+1))
    base_10 += int(digit) * num

print(base_10)

เพื่อให้เห็นภาพมากขึ้น เราจะเขียน Script เพื่อแปลงมันกลับไปเป็นเลขฐาน 10 กัน เราก็แค่เอามาทีละตำแหน่ง แล้วบวกไปเรื่อย ๆ เท่านั้นเลย ในที่นี้ base_2 เราก็จะเอาผลลัพธ์จากรอบที่เราแปลงรอบก่อนมาใส่ตรง ๆ เลย

0.899993896484375

เมื่อรันออกมา เราจะเห็นว่า อ้าว มันไม่ได้กลับไปเป็น 0.9 แต่ได้ออกมาเป็นเกือบ ๆ 0.9 นั่นก็เพราะอย่างที่เราบอกว่า มันวนไปเรื่อย ๆ แต่ตำแหน่งที่เราเก็บมันสั้นกว่านั้น มันเก็บได้จำกัด ทำให้เราไม่สามารถ Represent ค่าจริง ๆ ลงไปบนระบบฐาน 2 ได้ เลยต้องใช้เป็นแค่การประมาณเท่านั้น เราเลยเรียกว่า Floating Point Approximation

เราจะแก้ปัญหาอย่างไร

from decimal import Decimal

print(Decimal('0.3') + Decimal('0.6'))

สำหรับบน Python เขาเตรียม Package สำหรับการจัดการเรื่องแบบนี้โดยเฉพาะเลย แค่เราเรียกเป็น Decimal แต่นั้นเลย เราก็จะได้คำตอบที่ถูกต้อง

round(0.3+0.6,1)

อีกวิธีคือการ Round หรือการปัดนั่นเอา อย่างที่เราบอกว่า เราไม่สามารถเก็บค่าจริง ๆ ได้ งั้นเราก็เอาค่าเท่าที่เราเก็บได้แหละ มาปัด ก็เป็นอีกวิธีเหมือนกัน ซึ่งในหลาย ๆ ภาษาก็จะมีพวก Round Function มาด้วย ลองไปหาใช้ดูได้

สรุป

จำนวนทศนิยมเรียกว่าเป็นปัญหาสำหรับการคำนวณบนเครื่องคอมพิวเตอร์อยู่พอสมควรด้วยวิธีการที่เราใช้ในการ Represent ทศนิยมบนระบบคอมพิวเตอร์ ที่เรายังใช้เป็นเลขฐาน 2 แปลงมาเป็นฐาน 10 อีกที ซึ่งถามว่า คนทั่ว ๆ ไปมีปัญหาอะไรมั้ย เราก็ต้องบอกเลยว่า ไม่ เพราะเราไม่ได้ใช้ความละเอียดของทศนิยมมากขนาดนั้น เราแก้ปัญหาด้วยการปัดเลขได้ แต่สำหรับการคำนวณเฉพาะทางมาก ๆ อย่างในฝังของงานวิจัยทางวิทยาศาสตร์ต่าง ๆ เรื่องพวกนี้อาจจะเป็นปัญหาก็ได้ ซึ่งพวกนั้นเขาก็จะมีวิธีการดีลที่แตกต่างกัน เช่น อาจจะปัดเหมือนเราแหละ แต่จำนวนทศนิยมที่เขาปัด อาจจะมากกว่าเราเยอะมาก ๆ เพื่อให้การคำนวณมันละเอียดมากขึ้น เป็นเรื่องแปลก ๆ ที่เราว่า หลาย ๆ คนจนเจอเยอะมาก ๆ จนเป็นมีมเลย ก็หวังว่าจะเป็นประโยชน์กันนะครับ