ค่า PI กับความวนไม่รู้จบ

จากตอนที่แล้วเขียนเรื่องจำนวนเฉพาะเมื่อนานมาแล้ว เลยอยากเขียนอีกค่าที่สนุกไม่แพ้กันคือ ค่า PI เราอาจจะเคยได้ยินมาไม่มากก็น้อยอย่างน้อยก็น่าจะช่วงประถม มัธยม อะไรบ้างแหละ ที่เราใช้คำนวณพวก เส้นรอบวง และ พื้นที่ของวงกลม เราจำกันแค่ว่า มันคือ 3.14 แต่จริง ๆ แล้วมันเป็นลำดับของตัวเลขที่เจ๋งมาก ๆ เพราะจนตอนนี้ เราก็ยังหาไม่เจอว่า จริง ๆ แล้วมันมีค่าเท่าไหร่กันแน่

ค่า PI จริง ๆ คืออะไร ?

เราอาจจะคำแค่ว่า ค่า PI ประมาณได้ 3.14 แล้วจริง ๆ มันประมาณจากค่าอะไรกันแน่ ถ้าเราจะคุยกันเรื่องนี้ มันต้องย้อนไปไกลมาก ๆ แต่ ก็ไม่แน่ใจนะว่าใครเป็นคนที่คิดมันขึ้นมา

แต่ถ้าถามว่า ค่านี้มันคืออะไร มันก็คือ การเอา ความยาวของเส้นรอบวง หาร กับ ความยาวของเส้นผ่านศูนย์กลางหารกัน

ถ้าเอาวัดแบบตรง ๆ เลย เราก็น่าจะเอา วงกลมมาสักวง แล้วเอาเชือกมาพันรอบวงกลมนั้น เพื่อหาความยาวเส้นรอบวง และ เอาเชือกมาวัดความยาวเส้นผ่านศูนย์กลาง แล้วเอามาหารกันตามนิยาม ก็น่าจะได้สินะ แต่... มันจะดูลำบากเกินไปมั้ย มันมีวิธีการอย่างอื่นอีกมั้ย

เราจะหาค่า PI ยังไงดี ?

แล้วถ้าเราจะมาหาค่า PI กัน เราจะหาอย่างไร โอเค ถ้าเราไปหาในอินเตอร์เน็ต เราอาจจะเจอหลายวิธีมาก ๆ แต่เราอยากให้ลองเริ่มจากวิธีการแบบตรง ๆ กันก่อน

เราเริ่มจาก วงกลม สักอันนึง เรายกมาสักสูตร เป็นการหาพื้นที่ของวงกลมละกัน คือค่า PI คูณด้วย r หรือรัศมียกกำลัง 2 อาจจะงง งั้นเราลองวาดสี่เหลี่ยมจตุรัสครอบเข้าไป ทำให้ด้านกว้าง และ ยาว มันก็จะเป็น 2r เออ กว้างยาว มันก็ต้องเท่าสิ เพราะมันเป็นสี่เหลี่ยมจตุรัส

ถ้าเราจะหาพื้นที่ของสี่เหลี่ยมจตุรัสนี้ มันก็จะเป็น 2r ยกกำลังสอง มันก็จะได้เป็น 4 คูณกับ r ยกกำลัง 2 เราจะเห็นว่า มันมีความสัมพันธ์ของพื้นที่สี่เหลี่ยมจตุรัส และ พื้นที่ของวงกลม งั้นเรามาหาอัตราส่วนกัน

ทำให้เราจะได้ออกมาเป็น อัตราส่วนของพื้นที่วงกลม และ สี่เหลี่ยมจตุรัส เป็น PI คูณกับรัศมีของวงกลมยกกำลังสอง หารกับ 4 คูณด้วย r ยกกำลังสอง เราก็จะเห็นว่า มันมี r กำลังสองอยู่ เราก็สามารถตัดออกได้เลย ทำให้เราเหลือแค่ PI หารด้วย 4 เท่ากับ อัตราส่วนของพื้นที่วงกลม ต่อสี่เหลี่ยมจตุรัส

ถ้าเราแก้สมการย้ายข้างไป ๆ มา ๆ เราก็จะได้ค่า PI จะเท่ากับ อัตราส่วนของพื้นที่วงกลม ต่อสี่เหลี่ยมจตุรัส คูณกับ 4 อีกที แล้วถามว่า แล้วเราจะหาอัตราส่วนนี่ยังไงดีละ ตัวสี่เหลี่ยม อะ มันหาไม่ยาก แต่ วงกลม พื้นที่ถ้าเราจะหาสุดท้ายมันก็ต้องเป็น PI คูณกับ r ยกกำลังสองอยู่ดีมันก็วนกลับมาที่เดิม ดังนั้น เราหามันตรง ๆ ไม่ได้

งั้นถ้าเราลองสุ่มจุดลงไปในพื้นที่สักอันมั้ย ถ้าเราจุด ๆ ลงไปเยอะ ๆ มันก็จะเต็มพื้นที่ เราก็นับจุดที่อยู่ในวงกลม หารด้วย จุดทั้งหมด แล้วหารกัน เราก็น่าจะได้อัตราส่วนที่เราต้องการ และ คูณ 4 เราก็น่าจะได้ค่า PI ที่เราต้องการออกมา ดังนั้น ยิ่งถ้าเราสุ่มจุดเยอะมากเท่าไหร่ เราก็จะได้ค่าที่ใกล้เคียงกับค่าจริงมากขึ้นเรื่อย ๆ

Let's crunch some number

def one_unit_circle (n_count : int) :  
    total_points = 0
    total_circle_points = 0

เรามาลองเขียน Code กันเลยดีกว่า เราเขียนออกมาเป็น Function บน Python เรารับค่า n_count เป็นจำนวนครั้งในการสุ่มจุดลงไป จากนั้น เราก็จะกำหนดค่า จำนวนจุดที่อยู่ในวงกลม และ จุดทั้งหมด เป็น 0 เป็นการเริ่มต้น

for _ in range(n_count) :
        x = rnd.uniform(-1,1)
        y = rnd.uniform(-1,1)
        
        total_points += 1

แล้วเราจะเราจะเริ่ม Loop ตามจำนวนรอบที่เรากำหนดเข้ามาแล้ว ง่าย ๆ เลย ทำตามที่เราเล่าไป จะเริ่มจาก การสุ่มจุด X และ Y ใน 2D Plane ที่เราคิดกันไว้ ซึ่งเรากำหนดไว้เลยว่า รัศมีเป็น 1 หรือเราใช้ One Unit Circle ในการหา และวงกลม กับ สี่เหลี่ยม มันอยู่ตรงกลาง ทำให้ใน Plane ของเราจะ วิ่งตั้งแต่ -1 ถึง 1 ซึ่งเราจะใช้ Function ของ Random บน Python เองอย่าง uniform แล้วกำหนดค่าที่เราต้องการคือ -1 ถึง 1 เมื่อเราสร้างจุดขึ้นมาแล้ว เราก็นับจุดเข้าไป คือบวก 1 ไปตรง ๆ นี่แหละ

จากนั้น เราจะมาหาแล้วว่า จุดที่มันสุ่มขึ้นมา มันอยู่ในวงกลมหรือไม่ ถ้าไม่เราจะได้ไม่นับเข้าไป ถามว่า แล้วเราจะนับอย่างไรละ คิดง่าย ๆ คือ ถ้าเราวัดจากตรงกลางวงกลม จุดที่อยู่ในวงกลม จะต้องห่างไม่เกินรัศมี หรือ ในกรณีนี้คือ 1

โอเค แล้วเราจะรู้ได้อย่างไร ว่ามันมีระยะห่างจาก กลางวงกลม ไปที่จุด มันเป็นเท่าไหร่ ถ้าเราลองลากเส้นจากจุดไปที่จุดศูนย์กลางของวงกลม แล้วเทียบกับเส้นรัศมี เราจะเห็นว่า มันจะเป็นสามเหลี่ยมมุมฉาก เรารู้ 2 ด้าน ใช่แล้วฮ่ะ เราสามารถใช้ Pythagoras Theorem ในการหาได้ แก้สมการออกมา มันก็จะเป็น เอาจุด x ยกกำลังสอง แล้วบวกด้วย y ยกกำลังสอง

distance = x * x + y * y
        
if (distance < 1) :
    total_circle_points += 1

เราเอาสมการที่แก้เมื่อกี้เข้ามาเขียนแล้วยัดใส่ในตัวแปร distance และ เราก็เทียบกับรัศมีของวงกลม นั่นก็คือ 1 เพราะเราใช้ One Unit Circle ถ้าระยะมันน้อยกว่ารัศมี ก็คือมันอยู่ในวงกลม ถ้าอยู่ในวงกลม เราก็บวกจำนวนจุดเข้าไปอีก 1

pi = 4.0 * (total_circle_points / total_points)

สุดท้าย เราก็จะคำนวณค่า PI ได้ละ ทำตามที่เราคุยกันไว้ก่อนหน้าคือ การเอาจำนวนจุดในวงกลม หารจุดทั้งหมด และ คูณ 4 เข้าไป เราก็จะได้ออกมา

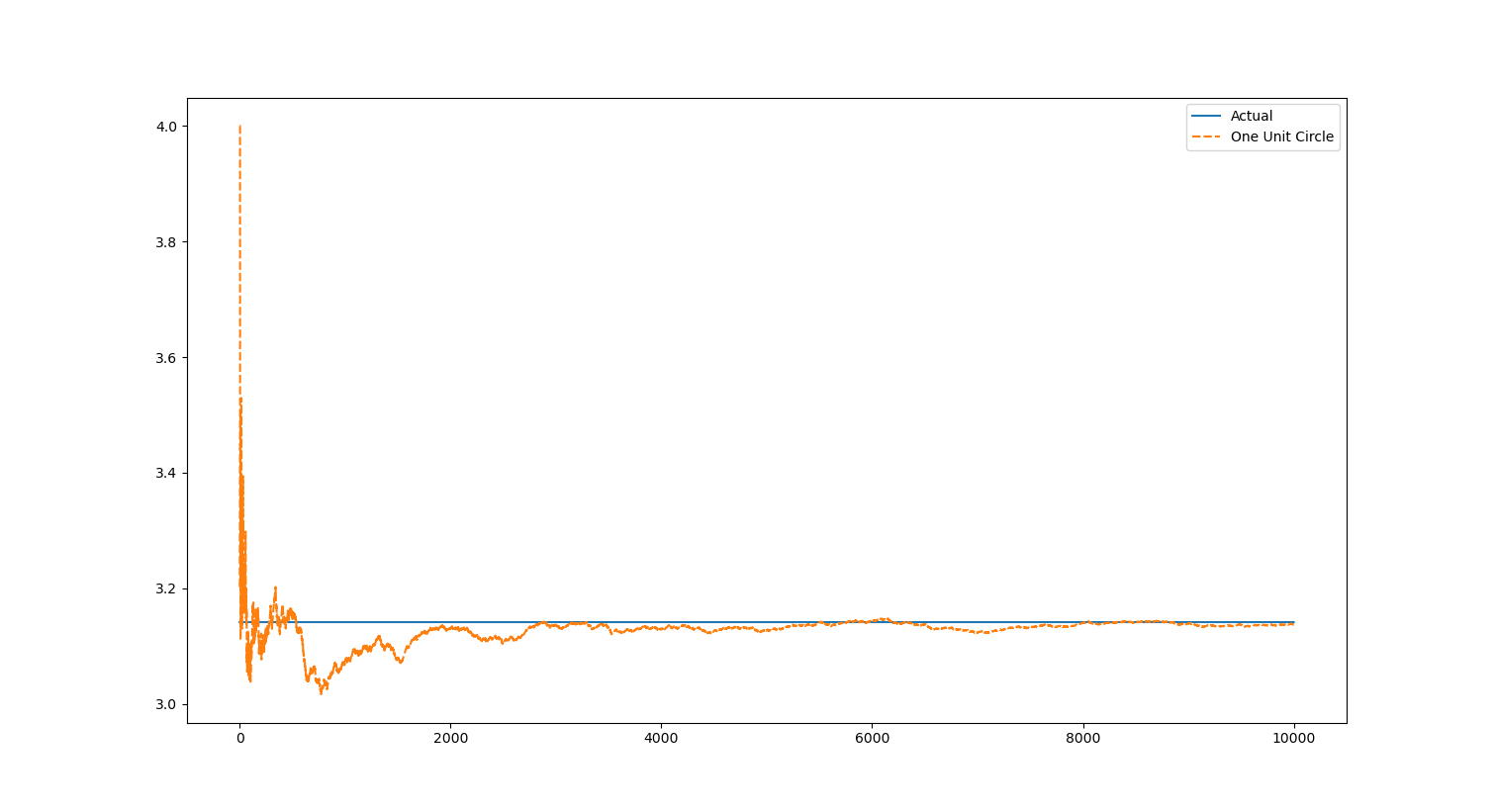
ถ้าเราลอง Plot ค่าที่ได้ในแต่ละรอบออกมา พร้อมกับค่าจริงที่ได้จาก Math Module เราจะเห็นว่า ค่าที่เราได้ออกมา มันจะเข้าใกล้ค่าจริงมากขึ้นเรื่อย ๆ แต่กว่ามันจะเข้าใกล้ค่าจริงได้ มันกดไป 8,000 รอบกว่า ๆ เลย ถ้าเราไม่ได้ต้องการความละเอียดอะไรสูงมาก การหาด้วยวิธีนี้มันก็พอได้อยู่แหละ

Can we go faster?

จากวิธีก่อนหน้า เราจะเห็นว่า กว่าที่เราจะได้ค่าที่เข้าใกล้กับค่าจริงมันใช้รอบเยอะมาก ๆ มันมีวิธีอื่นนอกจากวิธีนี้บ้างมั้ย

จริง ๆ แล้วการหาค่า Pi เป็นความท้าทายมาก ๆ เพราะมันเอามาใช้กับหลาย ๆ อย่างเยอะมาก ๆ ทำให้มีนักคณิตศาสตร์หลาย ๆ คน พยายามที่จะสร้างวิธีการที่เอามาหาค่า Pi ให้เร็วขึ้นเยอะมาก ๆ ต่างใช้ข้อสังเกตทางคณิตศาสตร์ต่าง ๆ อีกเยอะ เช่น Spigot Algorithm และที่เราใช้งานกันเยอะ ๆ จริง ๆ น่าจะเป็น Ramanujan's Formula อันนี้ก็คือ เกินความเข้าใจเราจริง ๆ ไว้ให้พวกคณิตศาสตร์มาอธิบายละกัน ยากเกินสำหรับเรามาก ๆ